2. 安徽省妇幼保健院检验科, 安徽 合肥 230001;
3. 安徽省妇幼保健院科教处, 安徽 合肥 230001
2. Department of Laboratory Medicine, Anhui Province Maternity and Child Health Hospital, Hefei 230001, China;
3. Department of Scientific Research and Education, Anhui Province Maternity and Child Health Hospital, Hefei 230001, China
细菌耐药已成为威胁人类健康最重要的公共卫生问题之一。耐药性变化或已成为细菌变异的自然过程之一,随着时间的推移,细菌不断发展出抵抗、逃避或保持对多种类抗菌药物抵抗机制[1]。细菌耐药率的增加不仅会引起更高的疾病发病率和死亡率,而且会导致更长的住院时间和更高的治疗费用[2-3]。研究[4]表明,我国每年约27.45%的住院患者发生耐药菌感染或定植,其中15.77%为多重耐药菌,2017年我国因细菌耐药性造成的社会经济负担约为770亿美元,占国内生产总值的0.37%,其中570亿美元与多重耐药菌有关。目前,世界各国主要通过对细菌耐药情况进行长期、动态地监测和分析,不断提升对细菌耐药性变迁的预警能力,并有针对性的加强对医疗、农业、环境等各领域抗菌药物使用的监管与指导,从而遏制细菌耐药率不断升高的现象[5]。世界卫生组织(WHO)认为加强抗菌药物管理及细菌耐药性监测是做好多重耐药菌防控的重要途径[6-7],我国已建立较为完善的从国家、各省份到各级医疗机构的细菌耐药监测网络,以充分掌握细菌耐药性的流行规律和传播特征,从监测结果来看,我国细菌耐药率仍然保持较高水平,细菌耐药防控形势依然严峻[8-9]。
为充分掌握细菌耐药性流行传播的系统规律和动态特征,定量分析是非常实用的方法,即通过构建反映细菌耐药性动态特征的数学模型,对动态特征进行分析、总结,并对未来的发展趋势进行预测,从而寻求预防和控制耐药细菌传播的最佳策略。由于本次研究是基于我国2014—2020年全国多重耐药菌监测数据,具有时间序列性、样本量小、建模信息少等特点,传统的建模方法很难达到较好的预测效果,相比之下,灰色预测GM(1, 1)模型可能是一种有效的替代方法,GM(1, 1)模型是灰色系统理论中最主要的单变量预测模型,是研究小数据、信息贫乏的不确定性问题的有效途径,可以对含有时间序列的原始数据进行处理,发现和掌握事物发展的规律,对未来的状态做出科学的定量预测,具有较高的预测精度[10],已广泛应用于自然科学和社会经济等各个领域。本研究主要通过构建灰色预测GM(1, 1)模型对我国几种常见细菌的耐药率进行预测,并进一步分析细菌耐药特征的变化趋势,为完善细菌耐药防控措施提供一定的数据支持,同时也将灰色预测模型介绍到医院感染防控领域,为医院感染防控提供一种可供选择的定量分析方法。
1 资料与方法 1.1 数据来源本研究数据源自全国细菌耐药监测网(CARSS,http://www.carss.cn/),该平台由国家卫生健康委组建,1 000多所成员单位,数据上报率超过99%。各成员单位所有革兰阳性菌和革兰阴性菌的临床分离株均采用统一方案进行收集和测定,根据美国临床和实验室标准化协会(CLSI)标准进行报告,数据真实可靠、可信度高。本次研究主要选取2014—2020年各年度全国细菌耐药监测报告(简要版)中总体耐药率或检出率较高的几种细菌,如耐甲氧西林金黄色葡萄球菌(MRSA)、耐碳青霉烯类铜绿假单胞菌(CRPA)和鲍曼不动杆菌(CRAB)、耐第三代头孢菌素的大肠埃希菌(3GCR-E.coli)和肺炎克雷伯菌(3GCR-KP)等进行分析预测。
1.2 研究方法本研究通过对2014—2018年全国细菌耐药监测报告中MRSA、CRPA、CRAB、3GCR-E.coli、3GCR-KP等细菌耐药率数据构建灰色预测GM(1, 1)模型,并用后验差比C值和小误差概率P值评估模型精度,用相对误差和级比偏差评估模型拟合效果。用2019—2020年耐药率数据验证GM(1, 1)模型的预测效果。最终根据所建模型对2021—2023年MRSA、CRPA、CRAB、3GCR-E.coli和3GCR-KP等5种细菌的耐药率进行预测,并基于预测结果分析细菌耐药率变化趋势。应用SPSS au在线分析软件进行模型建立、预测和拟合精度检验。
1.3 灰色预测模型的建立与计算方法GM(1, 1)模型主要是对原始数据作数据处理,对生成新的数据序列构建微分方程模型,获得微分方程的时间相应函数,再一次累减过程计算,最终获得原始序列模拟值。具体建模过程如下[11]:
(1) 假设原始序列:X(0)={x(0)(1), x(0)(2), …x(0)(n)},x(0)(k)≥0,k=1, 2, …, n。
(2) 通过对原始序列依次进行一阶累加,获得1-AGO序列X(0),X(1)={x(1)(1), x(1)(2), …x(1)(n)},其中
(3) 计算X(1)的紧邻均值生成序列:z(1)=(z(1)(1),z(1)(2), …,z(1)(n)),其中,z(1)(k)=
(4) 利用最小二乘法对a, b进行参数估计,获得
| $ \left[ {\begin{array}{*{20}{l}} a\\ b \end{array}} \right] = {\left( {{B^T}B} \right)^{ - 1}}{B^T}Y $ |
| $ B = \left[ {\begin{array}{*{20}{c}} { - {z^{(1)}}(2)}&1\\ { - {z^{(1)}}(3)}&{}\\ { \cdots \;\;\; \cdots }& \cdots \\ { - {z^{(1)}}(n)}&1 \end{array}} \right] $ |
| $ Y = \left[ {\begin{array}{*{20}{l}} {{x^{(0)}}}&{(2)}\\ {{x^{(0)}}}&{(2)}\\ \cdots & \cdots \\ {{x^{(0)}}}&{(n)} \end{array}} \right] $ |
(5) 在获得a, b参数估计值后,再代入GM(1, 1)模型的白化方程,即
(6) 由于上述时间响应序列为原始序列的一次累加序列,因此需再进行逆还原(一次累减过程)方可最终获得原始序列模拟值:
为检验GM(1, 1)模型的可靠性和预测准确性,需要对该模型进行拟合效果检验,若模型拟合度高,则可以认为模型预测误差小,模型可用于外推。若两者拟合度低,需对原始数据通过平移转换或残差修正后重新建立预测模型。通常可根据小误差概率P值、后验差比C值以及残差检验判断灰色预测模型的拟合效果,这些统计量在分析软件中均可获得。后验差比C值和小误差概率P值常用于模型精度等级检验,模型精度等级判断标准见表 1。模型残差检验用于检验模型拟合效果,主要指标包括相对误差和级比偏差,两个指标数值均越小越好,<0.1说明达到较高要求,0.1~0.2可以认为基本达到要求。
| 表 1 灰色预测GM(1, 1)模型精度等级判断标准 Table 1 Standards for precision grades of grey prediction GM (1, 1) model |
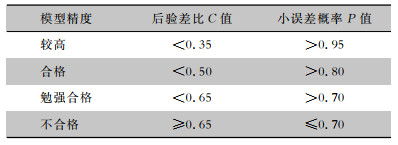
|
分别对MRSA检出率以及CRPA、CRAB、3GCR-E.coli、3GCR-KP检出率时间序列数据构建微分方程模型,通过计算可获得每个模型的发展系数-a和灰作用量b的参数估计值,见表 2,并最终获得5个GM(1, 1)模型的回归方程分别为:
| 表 2 GM(1, 1)模型参数估计值和预测精度检验 Table 2 Parameter estimation value and prediction precision test of GM (1, 1) model |
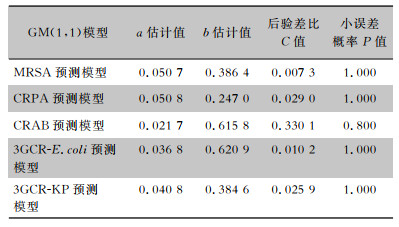
|
MRSA灰色预测GM(1, 1)模型:x(1)(k+1)=-7.261e-0.050 7k+7.621
CRPA灰色预测GM(1, 1)模型:x(1)(k+1)=-4.606e-0.050 8k+4.862
CRAB灰色预测GM(1, 1)模型:x(1)(k+1)=-27.808e-0.021 7k+28.378
3GCR-E.coli灰色预测GM(1, 1)模型:x(1)(k+1)=-16.275e-0.036 8k+16.872
3GCR-KP灰色预测GM(1, 1)模型:x(1)(k+1)=-9.057e-0.040 8k+9.426
2.2 5种细菌耐药率GM(1, 1)预测模型拟合效果根据表 1模型精度判定标准,对MRSA、CRPA、CRAB、3GCR-E.coli、3GCR-KP等5种细菌耐药率建立的GM(1, 1)模型,其拟合精度等级均较高,具体各模型的后验差比C值和小误差概率P值见表 2。由表 3可见,所有模型的相对误差值和级比偏差均<0.1,说明所有预测模型均有较高的拟合效果。
| 表 3 5种细菌耐药率GM(1, 1)预测模型残差检验结果 Table 3 Residual test results of GM (1, 1) prediction models for drug resistance rates of five types of bacteria |
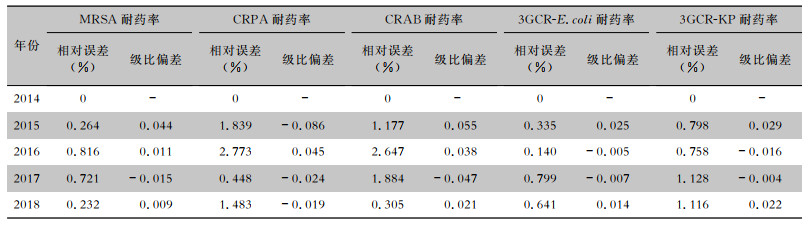
|
根据建立的灰色预测GM(1, 1)模型,可计算2019—2023年各多重耐药菌的耐药率预测值,见表 4。除2020年3GCR-E.coli耐药率预测值与实际值的绝对误差为2.7%以外,其他4种细菌2019、2020年耐药率预测绝对误差均在2%以内,部分预测误差可控制在1%以内。可以认为本研究建立的所有GM(1, 1)模型预测误差均较小,模型可用于外推预测。结合图 1可见,总体上2014—2023年,我国MRSA、CRPA、CRAB、3GCR-E.coli、3GCR-KP 5种多重耐药菌的耐药率呈下降趋势,根据预测2023年其耐药率分别可降低至23.9%、15.2%、50.2%、43.8%、26.1%。
| 表 4 GM(1, 1)预测模型预测的各多重耐药菌耐药率及实际耐药率(%) Table 4 Drug resistant rates and actual resistant rates of MDRO5 predicted with GM (1, 1) prediction models(%) |
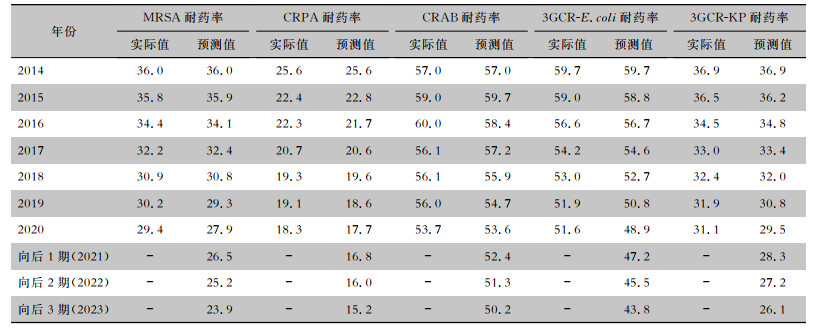
|
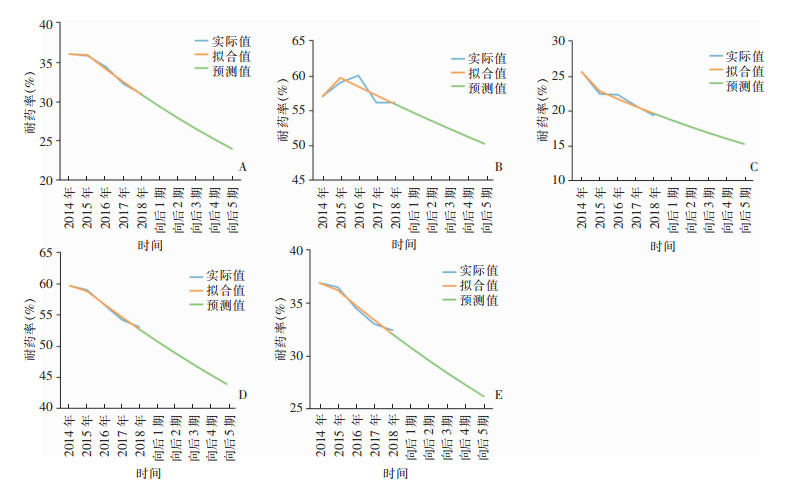 |
| 注:A为MRSA;B为CRAB;C为CRPA;D为3GCR-E.coli;E为3GCR-KP。 图 1 5种细菌耐药率模型拟合及预测效果图 Figure 1 Fitting and prediction effectiveness of drug resistance rate models for 5 types of bacteria |
细菌耐药监测数据表明,我国仍然是受细菌耐药威胁最严重的国家之一,细菌耐药性依然高水平流行。但是,通过本次研究发现,总体上我国细菌耐药性呈现不断降低的趋势,MRSA、CRPA、CRAB、3GCR-E.coli、3GCR-KP耐药率分别从2014年的36.0%、25.6%、57.0%、59.7%、36.9%降低至2020年的29.4%、18.3%、53.7%、51.6%、31.1%。同时根据本研究预测,到2023年上述5种耐药菌的耐药率可分别降至23.9%、15.2%、50.2%、43.8%、26.1%,说明经过多年努力,我国在细菌耐药性防控方面成效显著。这种下降趋势可能与以下方面有关:其一,各级政府部门对医疗卫生、农业、环境等领域抗菌药物的生产、流通、应用等各个环节持续强化监督管理。其次,我国建立完善的国家层面、省级层面和医疗机构层面的三级感染监测控制体系,逐步实现全国范围内医疗机构感染前瞻性目标监测,不断规范抗菌药物的合理使用,如2019年国家卫生健康委《关于进一步加强医疗机构感染预防与控制工作的通知》,明确规定逐步实现全国范围内医疗机构感染前瞻性目标监测,并通过动态分析感染病原菌菌谱和耐药趋势变化,规范抗菌药物的合理使用等。第三,医院层面细菌耐药性监测网的全面建设,医疗机构实验室对细菌耐药性的监测能力和药敏鉴定水平不断提升,能够为临床医生合理选择治疗方案和抗感染策略起到重要保障作用[12-13]。
虽然通过模型预测发现我国多种细菌耐药性有不断下降的趋势,但必须清醒的认识到我国的细菌耐药性仍处于高位流行的水平,中国仍然是抗菌药物消费大国,与国外相比,抗菌药物的可及性和销售量依然较高,关于抗菌药物使用的循证依据尚未完全被卫生专业人员广泛接受等事实[8]。其次在临床抗菌药物的管理方面仍然局限于临床教育、行政命令和监督检查为主,需要进一步探索适当的激励措施,以达到长期、有效、可持续性改善抗菌药物管理现状的目标[14]。
时间序列预测是指利用前期的数据信息预测系统未来值的过程,文献中常用的基于统计模型和人工智能方法的时间序列分析对于非线性问题的预测并不准确,更重要的是它们需要大量的训练样本来提供信息从而构建模型,无法用于对小样本、贫信息数据的建模[15],而灰色系统理论的建模优势正好弥补了此缺陷,GM(1, 1)是灰色系统中最基本的预测模型,是灰色系统理论体系中的最重要方法之一,其模型表达方式为一阶方程和单变量,可以对含有时间序列的原始数据进行处理,该模型对样本含量和概率分布无严格要求[16],因此在对建模信息少、样本量小的数据序列进行预测时,具有较高的应用价值[17]。在本研究中,针对2014—2020年细菌耐药率的时间序列,已知的仅为耐药率和时间,其他影响因素的信息依然未知,显然,灰色预测GM(1, 1)模型是合适的。结果表明,本次建立的所有模型其精度等级和拟合效果均较好,能够准确预测耐药率,说明建立的GM(1, 1)模型在实践中是可信、有效的,能够为各级卫生行政部门和医疗机构及时研判细菌耐药分布情况和流行趋势,为及时调整防控策略和干预措施提供科学依据和数据支持, 同时卫生管理人员和医务工作者还能够根据最新的监测数据及时更新预测模型,以便进行长期分析与预测。
本文介绍的GM(1, 1)模型作为一种实用的决策工具,在国内外医疗卫生领域已得到广泛应用,如在传染病防控、慢性病管理、职业健康管理、流行病学研究等方面均有文献报道[18-21]。同时,该模型在医院感染防控方面,如对医疗机构各类医院感染发生率、多重耐药菌感染率、手卫生依从率以及医疗废物管理等预测和高风险因素探索等方面或亦有重要价值。
利益冲突:所有作者均声明不存在利益冲突。
| [1] |
Tacconelli E, Carrara E, Savoldi A, et al. Discovery, research, and development of new antibiotics: the WHO priority list of antibiotic-resistant bacteria and tuberculosis[J]. Lancet Infect Dis, 2018, 18(3): 318-327. DOI:10.1016/S1473-3099(17)30753-3 |
| [2] |
Founou RC, Founou LL, Essack SY. Clinical and economic impact of antibiotic resistance in developing countries: a systematic review and Meta-analysis[J]. PLoS One, 2017, 12(12): e0189621. DOI:10.1371/journal.pone.0189621 |
| [3] |
Teerawattanapong N, Panich P, Kulpokin D, et al. A systema-tic review of the burden of multidrug-resistant healthcare-associated infections among intensive care unit patients in Southeast Asia: the rise of multidrug-resistant Acinetobacter baumannii[J]. Infect Control Hosp Epidemiol, 2018, 39(5): 525-533. DOI:10.1017/ice.2018.58 |
| [4] |
Zhen XM, Stålsby Lundborg C, Sun XS, et al. Economic burden of antibiotic resistance in China: a national level estimate for inpatients[J]. Antimicrob Resist Infect Control, 2021, 10(1): 5. DOI:10.1186/s13756-020-00872-w |
| [5] |
邹胜男, 袁丽, 吕小艳, 等. 基于细菌耐药监测系统的多重耐药菌分析与对策[J]. 齐齐哈尔医学院学报, 2019, 40(13): 1656-1658. Zou SN, Yuan L, Lv XY, et al. Analysis and countermea-sures of multidrug-resistant bacteria based on bacterial resis-tance surveillance system[J]. Journal of Qiqihar Medical University, 2019, 40(13): 1656-1658. |
| [6] |
Taati Moghadam M, Khoshbayan A, Chegini Z, et al. Bacteriophages, a new therapeutic solution for inhibiting multidrug-resistant bacteria causing wound infection: lesson from animal models and clinical trials[J]. Drug Des Devel Ther, 2020, 14: 1867-1883. DOI:10.2147/DDDT.S251171 |
| [7] |
陈素明, 单斌, 王晓明, 等. 2018-2020年多中心多重耐药肠杆菌的流行病学特征及耐药性分析[J]. 中国抗生素杂志, 2021, 46(11): 1031-1037. Chen SM, Shan B, Wang XM, et al. Epidemiological characteristics and drug resistance analysis of multicenter and multi-drug resistant enterobacteria from 2018 to 2020[J]. Chinese Journal of Antibiotics, 2021, 46(11): 1031-1037. |
| [8] |
胡付品, 郭燕, 朱德妹, 等. 2018年CHINET中国细菌耐药性监测[J]. 中国感染与化疗杂志, 2020, 20(1): 1-10. Hu FP, Guo Y, Zhu DM, et al. CHINET surveillance of bacterial resistance in China: 2018 report[J]. Chinese Journal of Infection and Chemotherapy, 2020, 20(1): 1-10. |
| [9] |
全国细菌耐药监测网. 全国细菌耐药监测网2014-2019年细菌耐药性监测报告[J]. 中国感染控制杂志, 2021, 20(1): 15-30. China Antimicrobial Resistance Surveillance System. Antimicrobial resistance of bacteria: surveillance report from China Antimicrobial Resistance Surveillance System in 2014-2019[J]. Chinese Journal of Infection Control, 2021, 20(1): 15-30. |
| [10] |
Li H, Zeng B, Wang JZ, et al. Forecasting the number of new coronavirus infections using an improved grey prediction model[J]. Iran J Public Health, 2021, 50(9): 1842-1853. |
| [11] |
曾丹. 灰色预测模型的数据处理技术及其应用研究[D]. 南充: 西华师范大学, 2019. Zeng D. Data processing technology of grey forecast model and its application research[D]. Nanchong: China West Normal University, 2019. |
| [12] |
孟雪斐, 张鸿娟, 马志刚, 等. 2018-2020年多中心血流感染分离菌分布及耐药性分析[J]. 中国抗生素杂志, 2021, 46(11): 985-993. Meng XF, Zhang HJ, Ma ZG, et al. Distribution and drug resistance analysis of bacteria from bloodstream infection of multicenters from 2018 to 2020[J]. Chinese Journal of Antibio-tics, 2021, 46(11): 985-993. |
| [13] |
Hu FP, Zhu DM, Wang F, et al. Current status and trends of antibacterial resistance in China[J]. Clin Infect Dis, 2018, 67(Suppl 2): S128-S134. |
| [14] |
Cui D, Liu XL, Hawkey P, et al. Use of and microbial resis-tance to antibiotics in China: a path to reducing antimicrobial resistance[J]. J Int Med Res, 2017, 45(6): 1768-1778. |
| [15] |
Amigó JM, Hirata Y, Aihara K. On the limits of probabilistic forecasting in nonlinear time series analysis Ⅱ: differential entropy[J]. Chaos, 2017, 27(8): 083125. |
| [16] |
Wang YW, Shen ZZ, Jiang Y. Comparison of ARIMA and GM (1, 1) models for prediction of hepatitis B in China[J]. PLoS One, 2018, 13(9): e0201987. |
| [17] |
Ceylan Z, Bulkan S, Elevli S. Prediction of medical waste gene-ration using SVR, GM (1, 1) and ARIMA models: a case study for megacity Istanbul[J]. J Environ Health Sci Eng, 2020, 18(2): 687-697. |
| [18] |
Guo XJ, Shen HX, Liu SF, et al. Predicting the trend of infectious diseases using grey self-memory system model: a case study of the incidence of tuberculosis[J]. Public Health, 2021, 201: 108-114. |
| [19] |
Şahin U, Şahin T. Forecasting the cumulative number of confirmed cases of COVID -19 in Italy, UK and USA using fractional nonlinear grey Bernoulli model[J]. Chaos Solitons Fractals, 2020, 138: 109948. |
| [20] |
Zeng B, Yang YJ, Gou XY. Research on physical health early warning based on GM (1, 1)[J]. Comput Biol Med, 2022, 143: 105256. |
| [21] |
Cheng TT, Bai Y, Sun XZ, et al. Epidemiological analysis of varicella in Dalian from 2009 to 2019 and application of three kinds of model in prediction prevalence of varicella[J]. BMC Public Health, 2022, 22(1): 678. |



